Please tell me what you thought about this blog. Comments, suggestions and views are welcomed.
這是留言板-既然來了，就留個言再走吧！
由 養花種魚數月亮賞星星 於 2029年7月22日星期日
下午2:43 發表
Please tell me what you thought about this blog. Comments, suggestions and views are welcomed.
Mathematica 教學：Dijkstra Algorithm
由 戴忠淵 於 2024年11月24日星期日
下午4:26 發表
Concise and elegant!
g=Graph[
{1\[DirectedEdge]2,1\[DirectedEdge]3,2\[DirectedEdge]3,
2\[DirectedEdge]4,3\[DirectedEdge]5,4\[DirectedEdge]3,
4\[DirectedEdge]5,4\[DirectedEdge]6,5\[DirectedEdge]6},
EdgeWeight->{1,12,9,3,5,3,13,15,4},
EdgeLabels->Rule@@@Transpose@{
{1\[DirectedEdge]2,1\[DirectedEdge]3,2\[DirectedEdge]3,
2\[DirectedEdge]4,3\[DirectedEdge]5,4\[DirectedEdge]3,
4\[DirectedEdge]5,4\[DirectedEdge]6,5\[DirectedEdge]6},
{1,12,9,3,5,3,13,15,4}},
VertexStyle->Yellow,VertexSize->0.5,
VertexShapeFunction->{{Yellow,Disk[#1,0.1],Black,Text[#2,#1]}&}]
route={{1,2,1},{1,3,12},{2,3,9},{2,4,3},{3,5,5},{4,3,4},{4,5,13},{5,6,4},{4,6,15}};
myroute=Select[Table[Select[route,#[[2]]==z&],{z,1,6}],#=!={}&]
Table[Set[v[temp],
SortBy[If[#[[1]]==1,{v[temp],#[[3]]},{v[temp],v[#[[1]]]+#[[3]]}]&/@
Select[Flatten[myroute,1],#[[2]]==temp&],Last][[1,2]]],{temp,2,6}]&/@Range[2]
Finally, the first acceptance of 2024 comes.
由 戴忠淵 於 2024年1月5日星期五
下午3:32 發表
A Sustainable Dynamic Optimization Model of Pricing and Advertising in the Presence of Green Innovation Investment
Chung-Yuan Dye and Tsu-Pang Hsieh
Finally, the acceptance from EJOR has arrived. The Julia code for the numerical examples in this paper is provided below. Alternatively, you can also implement it directly in Julia. Please leave a message if you have any problems with the implementation of the code.
julia=StartExternalSession["Julia"]
ExternalEvaluate[julia,"
using JuMP,Ipopt
dp(x)=(140-3*x);
K1(y)=(y/5-y^2/1000);
f1(x)=100*exp(-0.03*x);
f2(x)=2*exp(-0.045*x);
v1=25;
v2=10;
omega=300;
c=16.5;
h=0;
z=0.8;
"];
dynCP11=ExternalEvaluate[julia, "
function dynCP11(G0,gamma1,gamma2,delta,k1coef,k2coef,e,r,varpi,n)
m1 = Model(Ipopt.Optimizer)
set_silent(m1)
#set_optimizer_attributes(m1, \"tol\" => 1e-4, \"max_iter\" => 100)
register(m1, :dp, 1, dp; autodiff = true)
register(m1, :K1, 1, K1; autodiff = true)
register(m1, :f1, 1, f1; autodiff = true)
register(m1, :f2, 1, f2; autodiff = true)
@variable(m1, p[1:n], start = 30)
@variable(m1, w[1:n], start = 10)
@variable(m1, u[1:n], start = 10)
@NLexpression(m1,newG[i=1:n],(1-delta)^(-1+i)*((1-delta)*G0
+sum((gamma1*u[j+1]^k1coef+gamma2*w[j+1]^k2coef)/((1-delta)^j)
for j = 0:i-1)))
@NLexpression(m1,newCE[i=1:n],f1(w[i])+f2(w[i])*dp(p[i])*K1(newG[i])-varpi)
@NLobjective(
m1,
Max,
sum(z^(i-1)*((p[i]-c-h/2)*dp(p[i])*K1(newG[i])
-v1*u[i]^2/2-v2*w[i]^2/2-e*newCE[i])
for i = 1:n))
for i = 1:n
@constraint(m1, p[i] >= c + h / 2)
end
for i = 1:n
@constraint(m1, p[i] <= 140 / 3)
end
for i = 1:n
@constraint(m1, w[i] >= 0)
end
for i = 1:n
@constraint(m1, u[i] >= 0)
end
for i = 1:n
@NLconstraint(m1, newCE[i] >= 0)
end
JuMP.optimize!(m1)
p_val = JuMP.value.(p)
w_val = JuMP.value.(w)
u_val = JuMP.value.(u)
G_val=(1-delta)*G0+gamma1*u_val[1]^k1coef+gamma2*w_val[1]^k2coef
CE=f1(w_val[1])+f2(w_val[1])*dp(p_val[1])*K1(G_val)
profit=(p_val[1]-c-h/2)*dp(p_val[1])*K1(G_val)
-v1*u_val[1]^2/2-v2*w_val[1]^2/2-e*(CE-varpi)
return[p_val,w_val,u_val,G_val,CE,profit,objective_value(m1)]
end"];
dynCP22=ExternalEvaluate[julia,"
function dynCP22(G0,gamma1,gamma2,delta,k1coef,k2coef,e,r,varpi,n)
m1 = Model(Ipopt.Optimizer)
set_silent(m1)
#set_optimizer_attributes(m1, \"tol\" => 1e-4, \"max_iter\" => 100)
register(m1, :dp, 1, dp; autodiff = true)
register(m1, :K1, 1, K1; autodiff = true)
register(m1, :f1, 1, f1; autodiff = true)
register(m1, :f2, 1, f2; autodiff = true)
@variable(m1, p[1:n], start = 30)
@variable(m1, w[1:n], start = 10)
@variable(m1, u[1:n], start = 10)
@NLexpression(m1,newG[i=1:n],(1-delta)^(-1+i)*((1-delta)*G0
+sum((gamma1*u[j+1]^k1coef+gamma2*w[j+1]^k2coef)/((1-delta)^j)
for j = 0:i-1)))
@NLexpression(m1,newCE[i=1:n],f1(w[i])+f2(w[i])*dp(p[i])*K1(newG[i])-varpi)
@NLobjective(
m1,
Max,
sum(z^(i-1)*((p[i]-c-h/2)*dp(p[i])*K1(newG[i])
-v1*u[i]^2/2-v2*w[i]^2/2-r*newCE[i])
for i = 1:n))
for i = 1:n
@constraint(m1, p[i] >= c + h / 2)
end
for i = 1:n
@constraint(m1, p[i] <= 140 / 3)
end
for i = 1:n
@constraint(m1, w[i] >= 0)
end
for i = 1:n
@constraint(m1, u[i] >= 0)
end
for i = 1:n
@NLconstraint(m1, newCE[i] <= 0)
end
JuMP.optimize!(m1)
p_val = JuMP.value.(p)
w_val = JuMP.value.(w)
u_val = JuMP.value.(u)
G_val=(1-delta)*G0+gamma1*u_val[1]^k1coef+gamma2*w_val[1]^k2coef
CE=f1(w_val[1])+f2(w_val[1])*dp(p_val[1])*K1(G_val)
profit=(p_val[1]-c-h/2)*dp(p_val[1])*K1(G_val)
-v1*u_val[1]^2/2-v2*w_val[1]^2/2-r*(CE-varpi)
return[p_val,w_val,u_val,G_val,CE,profit,objective_value(m1)]
end"];
mysol13[g0_,\[Gamma]1_,\[Gamma]2_,\[Delta]_,k1_,k2_,e_,r_,cap_]:=
Block[{n=40,numiter=100,iter=0,ans1,ans2},
Print[{Dynamic[iter],Dynamic[ans2]}];
NestList[(
iter=iter+1;
ans1=
SortBy[{
dynCP11[#[[4]],\[Gamma]1,\[Gamma]2,\[Delta],k1,k2,e,r,cap,n],
dynCP22[#[[4]],\[Gamma]1,\[Gamma]2,\[Delta],k1,k2,e,r,cap,n]},
Last][[-1]];
ans2={ans1[[1,1]],ans1[[2,1]],ans1[[3,1]],ans1[[4]],
ans1[[5]],#[[-1]]+0.8^(iter-1)*ans1[[6]]})&,
{0,0,0,g0,0,0},numiter][[2;;-1]]
]
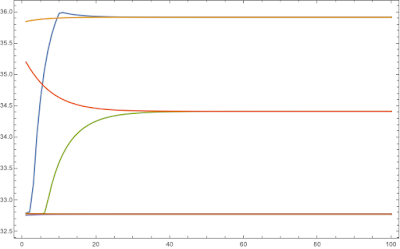
myexample=mysol13[#[[1]],0.5,0.8,0.2,0.5,0.8,8,2,#[[2]]]&/@
Flatten[Table[{i,j},{j,{250,300,400}},{i,{10,40}}],1]
ListLinePlot[myexample[[All,All,#]],PlotRange->All,
Frame->True]&/@{1,2,3,4,5}//Column
Mathematica 教學：Text arrangement
由 戴忠淵 於 2023年12月25日星期一
下午11:28 發表
test=ImageData[Rasterize["50",RasterSize->50,ImageSize->200]]
data=ParallelTable[{i,j,If[Mean@test[[i,j]]>0.95,0,1]},
{i,Dimensions[test][[1]]},{j,Dimensions[test][[2]]}]
picdata=Table[ParallelMap[If[#[[-1]]==0,"",
ImageResize[Import[RandomChoice[FileNames["*.jpeg",
"/Users/chungyuandye/Pictures/照片圖庫V4.photoslibrary/originals/",Infinity]]],{100,100}]]&,
data[[i]]],{i,54}]
GraphicsGrid[picdata]
Tikz: Drawing Random Circles with Randomly Assigned Centers and Radii
由 戴忠淵 於 2023年4月7日星期五
上午11:45 發表
\documentclass{article}
\usepackage{tikz}
\usepackage{adjustbox}
\begin{document}
\begin{center}
\begin{adjustbox}{width=0.6\textwidth}
\begin{tikzpicture}
\pgfmathsetseed{42}
\foreach \i in {1,...,500}
{
\pgfmathsetmacro{\a}{int(random(0,255))}
\pgfmathsetmacro{\b}{int(random(0,255))}
\pgfmathsetmacro{\c}{int(random(0,255))}
\pgfmathsetmacro{\r}{rand*2}
\pgfmathsetmacro{\x}{random(-10,10)}
\pgfmathsetmacro{\y}{random(-10,10)}
\definecolor{mycolor}{RGB}{\a,\b,\c}
\fill[mycolor] (\x,\y) circle (\r cm);
}
\end{tikzpicture}
\end{adjustbox}
\end{center}
\end{document}
Mathematica 教學：Call Julia from Mathematica
由 戴忠淵 於 2023年2月20日星期一
下午10:41 發表
session=StartExternalSession["Julia"]
test =
"function testpi(size)
sample = rand(size, 2)
dist = broadcast(hypot, sample[:,1], sample[:,2])
return sample, dist
end";
pitest=ExternalEvaluate[session,test]
size=100000
data=pitest[size];
ListPlot[GatherBy[Transpose[data[[1]]],Norm[#]<1&],Frame ->True,AspectRatio -> 1]
Length@GatherBy[Transpose[data[[1]]], Norm[#]<1&][[1]]/size//N
\documentclass[tikz]{standalone}
\usepackage{tikz}
\usepackage{ifthen}
\begin{document}
\begin{tikzpicture}
\draw[help lines, color=gray!30, dashed] (-1.2,1.5) grid (-1.2,1.5);
\draw[->] (-1.2,0)--(1.1,0) node[right]{$x$};
\draw[->] (0,-1.2)--(0,1.5) node[above]{$y$};
\draw[domain=0:1, smooth, variable=\x, black] plot ({\x}, {sqrt(1-\x*\x)});
\pgfmathsetseed{42}
\foreach \i in {1,...,10000}
{
\pgfmathsetmacro{\x}{abs(rand)}
\pgfmathsetmacro{\y}{abs(rand)}
\pgfmathsetmacro{\r}{\x*\x+\y*\y}
\pgfmathsetmacro{\col}{ifthenelse(\r<1,"blue!90","red!90")}
\fill[\col] (\x,\y) circle (0.1pt)
;
}
\end{tikzpicture}
\end{document}
Mathematica 教學：Policy function iterations for deterministic cake eating problem
由 戴忠淵 於 2023年2月12日星期日
下午4:54 發表
Policy function iterations方法是通過計算出最佳化問題的每一步所實現的最佳結果，並將這些結果用於計算下一步的最佳結果。此過程在一定數量的迭代後會得到一個最佳策略，並且這個策略也是最終的最佳解。因此它對於解決複雜的最佳化問題非常有用。它可以被用於解決各種經濟學、工程學和其他領域的最佳化問題。
繼續閱讀全文 Mathematica 教學：Policy function iterations for deterministic cake eating problem
ClearAll["Global`*"]
\[Alpha]=0.3;
\[Beta]=0.95;
\[Delta]=0.1;
\[Sigma]=1.5;
size=99;
K=Range[0.1,5,4.9/(size)];
V=Table[0,{size}];
astHoward=With[{n=size},
obj=ParallelTable[If[i^\[Alpha]+(1-\[Delta])*i-j<0,-10^9,
((i^\[Alpha]+(1-\[Delta])*i-j)^(1-\[Sigma])-1)/(1-\[Sigma])],
{i,0.1,5,4.9/n},{j,0.1,5,4.9/n}];
loops=0;
\[Epsilon]=99999;
Print[Grid[{
{"loop number ",
Dynamic[loops],
" with distance ",
Dynamic[NumberForm[\[Epsilon],
ExponentFunction->(If[-10<#<10,Null,#]&)]]}}]];
NestWhile[
NestWhile[
Transpose@
Table[{obj[[i,#[[2,i]]]]+\[Beta]*#[[1,#[[2,i]]]],#[[2,i]]},{i,Length[#[[1]]]}]&,
Transpose[SortBy[#,First][[-1]]&/@
Table[{obj[[i,j]]+\[Beta]*#[[1,j]],j},{i,n+1},{j,n+1}]//Parallelize],
Norm[#1[[1]]-#2[[1]]]>10^-6&,2]&,
{Table[0,n+1],Table[0,n+1]},
(loops++;\[Epsilon]=Norm[#1[[1]]-#2[[1]]];
Norm[#1[[1]]-#2[[1]]]>10^-6)&,2]
]
astHowardMatrix=With[{n=size},
obj=ParallelTable[If[i^\[Alpha]+(1-\[Delta])*i-j<
0,-10^9,((i^\[Alpha]+(1-\[Delta])*i-j)^(1-\[Sigma])-1)/(1-\[Sigma])],
{i,0.1,5,4.9/n},{j,0.1,5,4.9/n}];
loops=0;
\[Epsilon]=99999;
Id=IdentityMatrix[size+1];
Print[Grid[{
{"loop number ",
Dynamic[loops],
" with distance ",
Dynamic[NumberForm[\[Epsilon],
ExponentFunction->(If[-10<#<10,Null,#]&)]]}}]];
NestWhile[
(
myValue=Transpose[SortBy[#,First][[-1]]&/@
Table[{obj[[i,j]]+\[Beta]*#[[1,j]],j},{i,n+1},{j,n+1}]//Parallelize];
{Inverse[(Id-\[Beta]*Normal[SparseArray[
Rule[#,1]&/@Transpose[
{Range[size+1],myValue[[2]]}],size+1]])].(obj[[#[[1]],#[[2]]]]&/@
Transpose[{Range[size+1],myValue[[2]]}]),myValue[[2]]}
)&,
{Table[0,n+1],Table[0,n+1]},
(loops++;\[Epsilon]=Norm[#1[[1]]-#2[[1]]];
Norm[#1[[1]]-#2[[1]]]>10^-6)&,2]
]
ListLinePlot[astHowardMatrix[[1]],PlotRange->All,AspectRatio->1,Frame->True]
ListLinePlot[astHowardMatrix[[2]],PlotRange->All,AspectRatio->1,Frame->True]
Mathematica 教學：Value function iterations for deterministic cake eating problem
由 戴忠淵 於 2023年2月3日星期五
下午10:01 發表
ClearAll["Global`*"]
\[Alpha]=0.3;
\[Beta]=0.95;
\[Delta]=0.1;
\[Sigma]=1.5;
size=99;
K=Range[0.1,5,4.9/(size)];
V=Table[0,{size}];
ast=With[{n=size},
obj=
ParallelTable[
If[i^\[Alpha]+(1-\[Delta])*i-j<0,-10^9,
((i^\[Alpha]+(1-\[Delta])*i-j)^(1-\[Sigma])-1)/(1-\[Sigma])],
{i,0.1,5,4.9/n},{j,0.1,5,4.9/n}];
loops=0;
\[Epsilon]=99999;
Print[
Grid[{{"loop number ",Dynamic[loops]," with distance ",
Dynamic[NumberForm[\[Epsilon],
ExponentFunction->(If[-10<#<10,Null,#]&)]]}}]];
NestWhile[
Transpose[SortBy[#,First][[-1]]&/@Table[{obj[[i,j]]+\[Beta]*#[[1,j]],
Range[0.1,5,4.9/n][[j]]},{i,n+1},{j,n+1}]//Parallelize]&,
{Table[0,n+1],Table[0,n+1]},(loops++;\[Epsilon]=Norm[#1[[1]]-#2[[1]]];
Norm[#1[[1]]-#2[[1]]]>10^-6)&,2]
];
Mathematica 教學講義
由 戴忠淵 於 2022年5月25日星期三
下午11:50 發表
這是我這幾年來數量方法這一門課所自編的 Mathematica 入門教學講義。Mathematica 相較於其他軟體的特點在於強大的符號運算及動態幾何繪圖的科學運算能力。此外，Mathematica 尚包含數值運算、圖表可視化、動態操作介面等。由於擁有許多的內建程式語言及內建系統，故不需要繁雜且複雜的編寫，有能夠輕易上手的便利性。本教學講義相關檔案、資料檔及未來更新維護皆可由下列網址下載：
青春啊！
由 戴忠淵 於 2022年5月11日星期三
下午8:21 發表
帳號被盜走，上站6000次，我的青春啊！
2023年1月28日，失而復得。
用 JASP 輕鬆學 SEM:從基礎到應用
由 戴忠淵 於 2022年4月26日星期二
下午9:33 發表
JASP 統計軟體是由阿姆斯特丹大學 Eric-Jan Wagenmakers 教授領導的團隊，以 R 為核心所開發的
免費開源統計軟體，主要應用於心理及統計分析，相關的分析模組包含:平均數比較、實驗設計、迴歸與相關分析、探索性因素分析、驗證性因素分析（CFA）、結構方程式（SEM）、機械學習、神經網路等。
由於其設計理念為讓用戸熟悉並易於使用，故幾乎所有的分析模組都已視窗化，僅需要懂得相關的統計理論卽可輕易上手。有關 JASP 統計軟體的詳細説明可到官方網站參閲，https://jasp-stats.org/。JASP 統計軟體亦可由網站免費下載:
https://jasp-stats.org/download/
本年度統計分析教材以JASP 講義為主，JASP 統計軟體除了是免費開源外，該軟體以視窗的為主，學生只要能了解課堂上講授的統計分析及進階的驗證性因素分析、競爭模式、多群組比較、結構方程模型的理論後，卽可輕易執行上手。此外，JASP 統計軟體所産生的報表 及圖形皆以 APA 格式輸出，學生也能因此免除在茫茫報表中重新整理資料、繪製圖形，簡化發 表硏究成果及撰寫論文的流程。本教材相關檔案、資料檔及未來更新維護皆可由下列網址下載:https://github.com/chungyuandye/JASP-
Reduce PDF file size for Mac
由 戴忠淵 於 2022年1月28日星期五
下午10:03 發表
Mac PDF檔案縮小檔案大小：檔案➡輸出➡Quartz濾鏡➡Reduce file size。
111學測數A第18題
由 戴忠淵 於 2022年1月23日星期日
下午2:41 發表
利用三角板(30°-60°-90°)轉半圈即可。
pt[x0_]:={{0,0},{x0,Sqrt[4-x0^2]},{x,Sqrt[3-x^2]},{0,0}}/.
Quiet@Solve[{x^2+y^2==3,(x-x0)^2+(y-Sqrt[4-x0^2])^2==1},{x,y}][[2]]
Manipulate[
Plot[{Sqrt[4-x^2],Sqrt[3-x^2]},{x,-2,2},AspectRatio->1/2,
Epilog->{Green,Thickness[0.005],
Line[pt[Sqrt[3+10^(-7)]][[1;;3]]],
Red,PointSize[0.02],Point[pt[Sqrt[3+10^(-7)]]],
Point[pt[z][[1;;3]]],
Blue,Line[pt[z][[1;;2]]],Line[pt[z][[2;;3]]],
Line[pt[z][[3;;4]]]}
],{z,Sqrt[3]+10^(-7),-2}]
Integrate[Sqrt[4-x^2]-Sqrt[3-x^2],{x,0,Sqrt[3]}]
Integrate[Sqrt[4-x^2]-Sqrt[3](2+x),{x,-2,-(3/2)}]+
Integrate[Sqrt[4-x^2]-Sqrt[3-x^2],{x,-(3/2),Sqrt[3]}]//FullSimplify
Mathematica 教學：Factor analysis with Varimax rotation
由 戴忠淵 於 2021年7月8日星期四
下午2:49 發表
varimax[data_]:=Block[{AA,BB,CC,DD,nn,uu,XX,YY,vdata,angle,Tr,temp,vlist},
{nn,uu}=Dimensions[data];
vdata=Map[Normalize,data];
Do[
angle=Arg[nn* Total[Thread[Complex[
vdata[[All,iter[[1]]]],vdata[[All,iter[[2]]]]]]^4]
-Total[Thread[Complex[
vdata[[All,iter[[1]]]],vdata[[All,iter[[2]]]]]]^2]^2]/4;
Tr={{Cos[angle],-Sin[angle]},{Sin[angle],Cos[angle]}};
vdata[[All,iter]]= vdata[[All,iter]].Tr,
{iter,Flatten[Subsets[Range[uu],{2}]&/@Range[25],1]}
];
vdata*(Norm[#]&/@data)];
myfactor[data_]:=Block[{label,fadata,mypca,loadings,nf,rotatedloadings,
rotatedfactor,ncfa,proddata},
label=data[[1]];
fadata=data[[2;;-1]];
mypca=Eigensystem[Correlation@fadata];
nf=Length[Select[mypca[[1]],#>=1&]];
loadings=Transpose[mypca[[1,#]]^0.5*mypca[[2,#]]&/@Range[nf]];
rotatedloadings=varimax[loadings];
loadings=Flatten@{#,rotatedloadings[[#]],"",""}&/@Range[Length@loadings];
rotatedfactor=Table[Select[loadings,
(Abs[#[[i]]]==Max[Map[Abs,#[[2;;1+nf]]]])&],{i,2,nf+1}];
(rotatedfactor[[#,1,nf+2]]=mypca[[1,#]];
rotatedfactor[[#,1,nf+3]]=PercentForm[
Accumulate[mypca[[1]]][[#]]/Total[mypca[[1]]]];)&/@Range[nf];
Print["\n探索性因素分析\n"];
Print[TableForm[
Flatten[Table[Flatten@{StringReplace[label[[#[[1]]]]," "->""],
#[[2;;-1]]}&/@rotatedfactor[[i]],{i,nf}],1],
TableHeadings->{None,
Flatten@{"題項","因素"<>ToString[#]&/@Range[nf],"特徵根","解釋百分比"}}]];
ncfa=Length/@rotatedfactor;
proddata=data[[All,Flatten[#[[All,1]]&/@rotatedfactor]]][[2;;-1]];
Print["\n驗證性因素分析\n"];
Print@thesisnoworrycfa[
proddata,ncfa,ToExpression["X"<>ToString[#]]&/@Range[nf]];
];
myfactorcheck[data_]:=Block[{label,fadata,mypca,loadings,nf,
rotatedloadings,rotatedfactor,ncfa,proddata,check,checkfactornum},
label=data[[1]];
fadata=data[[2;;-1]];
mypca=Eigensystem[Correlation@fadata];
nf=Length[Select[mypca[[1]],#>=1&]];
loadings=Transpose[mypca[[1,#]]^0.5*mypca[[2,#]]&/@Range[nf]];
rotatedloadings=varimax[loadings];
loadings=Flatten@{#,rotatedloadings[[#]],"",""}&/@Range[Length@loadings];
rotatedfactor=Table[Select[loadings,(Abs[#[[i]]]==Max[Map[Abs,#[[2;;1+nf]]]])&],{i,2,nf+1}];
rotatedfactor=Table[Insert[i,Length[rotatedfactor[[#]]],-1],
{i,rotatedfactor[[#]]}]&/@Range[Length[rotatedfactor]];
check[list_,j_]:=Block[{temp=list},
If[Abs[temp[[1+j]]]<0 .45="" actor="" nf="" temp="">ToString[j];
temp[[3+nf]]="因素負荷過低",temp[[2+nf]]="Factor "<>ToString[j];
temp[[3+nf]]=temp[[3+nf]]];temp];
check=Flatten[Select[#,#[[-2]]=="因素負荷過低"||#[[-1]]<=2&]&/@Table[
Map[check[#,i]&,rotatedfactor[[i]]],{i,nf}],1];
Print@TableForm@check;
data[[All,Complement[Range[Dimensions[data][[2]]],check[[All,1]]]]]
];
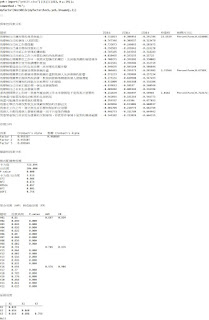
test=Import["test.xlsx"][[1]][[All,8;;29]];
semmethod="ML";
myfactor[NestWhile[myfactorcheck,test,UnsameQ,2]]
Mathematica 教學：Varimax rotation
由 戴忠淵 於 2021年7月4日星期日
上午9:24 發表
varimax[data_]:=
Block[{AA,BB,CC,DD,nn,uu,XX,YY,vdata,angle,Tr,temp,vlist},
{nn,uu}=Dimensions[data];
vdata=Map[Normalize,data];
Do[angle=Arg[nn*
Total[Thread[Complex[vdata[[All,iter[[1]]]],
vdata[[All,iter[[2]]]]]]^4]-
Total[Thread[Complex[vdata[[All,iter[[1]]]],
vdata[[All,iter[[2]]]]]]^2]^2]/4;
Tr={{Cos[angle],-Sin[angle]},{Sin[angle],Cos[angle]}};
vdata[[All,iter]]=vdata[[All,iter]].Tr,
{iter,Flatten[Subsets[Range[uu],{2}]&/@Range[25],1]}];
vdata*(Norm[#]&/@data)
]
L = {{-0.18444, 0.766739, -0.27758, 0.115158, 0.712221},
{0.698485, -0.30363, -0.19539, -0.2648, 0.688367},
{0.754094, 0.348652, -0.20205, -0.30588, 0.824599},
{0.365978, 0.162525, -0.1973, 0.849845, 0.92152},
{0.5781630, .044134, 0.452722, 0.157895, 0.566108},
{0.299667, 0.030388, 0.770856, 0.063739, 0.689006},
{0.817187, 0.239353, -0.19451, -0.16643, 0.79062},
{0.687893, 0.035304, 0.116032, 0.117627, 0.501742},
{0.301458, -0.74108, -0.3442, 0.233979, 0.81329}};
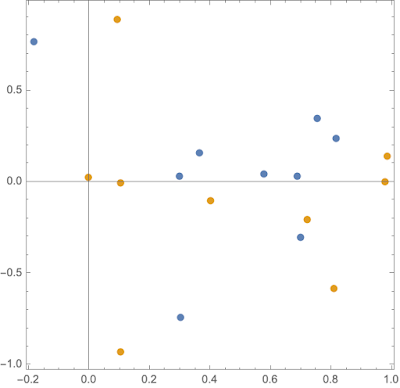
Map[NumberForm[#,{4,3}]&,varimax[L[[All,1;;4]]],{2}]//TableForm
(* Park, T. (2010). A Note on Terse Coding of Kaiser’s Varimax
Rotation Using Complex Number Representation.*)
Mathematica 教學：Convex Hull
由 戴忠淵 於 2020年8月25日星期二
下午2:09 發表
splitdata[datatemp___]:=Block[{eqn,temp,x,y,group,vertex,ans},
temp=SortBy[datatemp,Left][[{1,-1}]];
eqn[x_,y_]=y-temp[[1,2]]-
(temp[[1,2]]-temp[[2,2]])/(temp[[1,1]]-temp[[2,1]])(x-temp[[1,1]]);
group={Select[datatemp,eqn[#[[1]],#[[2]]]> 0&],
Select[datatemp,eqn[#[[1]],#[[2]]]< 0&]};
vertex={SortBy[group[[1]],Abs@eqn[#[[1]],#[[2]]]&][[-1]],
SortBy[group[[2]],Abs@eqn[#[[1]],#[[2]]]&][[-1]]};
ans={{{temp[[1]],vertex[[1]]},
Select[group[[1]],RegionMember[
Polygon[Insert[temp,vertex[[1]],-1]],#]==False&&#[[1]]< vertex[[1,1]]&]},
{{temp[[2]],vertex[[1]]},
Select[group[[1]],RegionMember[
Polygon[Insert[temp,vertex[[1]],-1]],#]==False&&#[[1]]> vertex[[1,1]]&]},
{{temp[[1]],vertex[[2]]},
Select[group[[2]],RegionMember[
Polygon[Insert[temp,vertex[[2]],-1]],#]==False&&#[[1]]< vertex[[2,1]]&]},
{{temp[[2]],vertex[[2]]},
Select[group[[2]],RegionMember[
Polygon[Insert[temp,vertex[[2]],-1]],#]==False&&#[[1]]> vertex[[2,1]]&]}
};
If[Length[#[[2]]]==0,{#[[1]],{#[[1,1]]}},{#[[1]],#[[2]]}]&/@ans
];
convexhull[{p1__,p2__},datatemp___]:=Block[{eqn,temp,x,y,group,vertex,ans},
temp=SortBy[{p1,p2},Left];
If[Length[datatemp]==0,{{temp,{}},{temp,{}}},
If[Length[datatemp]==1,{{{temp[[1]],datatemp[[1]]},{}},
{{temp[[2]],datatemp[[1]]},{}}},
eqn[x_,y_]=y-temp[[1,2]]-(temp[[1,2]]-temp[[2,2]])/
(temp[[1,1]]-temp[[2,1]])(x-temp[[1,1]]);
vertex=SortBy[datatemp,Abs@eqn[#[[1]],#[[2]]]&][[-1]];
group={Select[datatemp,#[[1]]< vertex[[1]]&],
Select[datatemp,#[[1]] > vertex[[1]]&]};
ans={{{temp[[1]],vertex},
Select[group[[1]],RegionMember[Polygon[Insert[temp,vertex,-1]],#]==
False&&#[[1]]< vertex[[1]]&]},
{{vertex,temp[[2]]},
Select[group[[2]],RegionMember[Polygon[Insert[temp,vertex,-1]],#]==
False&&#[[1]]> vertex[[1]]&]}}
]]
];
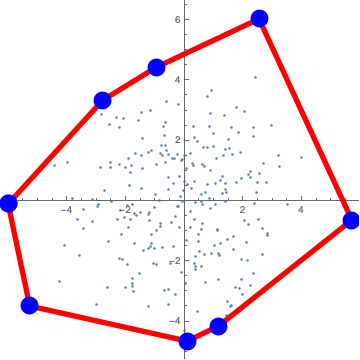
data=RandomReal[NormalDistribution[0,2],{250,2}];
Needs["ComputationalGeometry`"]
test=splitdata[data];
xx=Nest[Flatten[convexhull@@@#,1]&,test,3];
myline=Line/@Tally[xx[[All,1]]][[All,1]];
mypts=Point@Tally[xx[[All,1]]][[All,1,1]];
ListPlot[data,AspectRatio->1,
Epilog->{Red,Thickness[0.015],myline,Blue,PointSize[0.05],mypts}]
ThesisNoWorries Beta 0.3
由 戴忠淵 於 2020年8月3日星期一
下午8:45 發表
論文統計分析免煩惱，平均數比較、迴歸分析、信度、效度 CFA、結構方程是模型 SEM，一鍵搞定！
範例：本研究採量化研究，以XXX為研究對象，發放問卷XXX份，回收有效問卷XXX份，並以三山出版社所提供的 ThesisNoWorries 論文統計分析免煩惱 統計套件進行描述性統計、信效度分析、平均數比較、迴歸和相關分析、及結構方程式模型分析。
Excel：Calculate ACF and PACF in Excel
由 戴忠淵 於 2020年3月13日星期五
上午11:57 發表
Function acf(data As Range, k As Integer) As Double
Dim n As Integer
n = data.Rows.Count
Dim xbar As Double
xbar = Application.Average(data)
Dim sum1 As Double
sum1 = Application.SumProduct(data, data) - n * xbar * xbar
Dim sum2 As Double
sum2 = 0
For i = 1 To n - k
sum2 = sum2 + (data.Cells(i) - xbar) * (data.Cells(i + k) - xbar)
Next
acf = sum2 / sum1
End Function
Function pacf(data As Range, k As Integer) As Double
Dim xx() As Double
ReDim xx(1 To k, 1 To k) As Double
For i = 1 To k
For j = 1 To k
xx(i, j) = acf(data, Abs(j - i))
Next
Next
Dim yy() As Double
ReDim yy(1 To k, 1 To 1) As Double
For i = 1 To k
For j = 1 To 1
yy(i, 1) = acf(data, Abs(i))
Next
Next
pacf = Application.Index(Application.MMult(Application.MInverse(xx), yy), k, 1)
End Function
Exporting graphics to TikZ format with Mathematica, Version 2
由 戴忠淵 於 2020年2月3日星期一
下午12:05 發表
mytwoaxistikz[data__,{xmin_,xmax_,ymin_,ymax_},
mycolor__,{xlabel_,ylabel_},{rticks__,decimalr_,lticks__,decimall_},
linelabel__,linepos__,plotaspectratio_:1]:=Block[{temp=data,axis1,axis2,textpos,line},
axis1="
\\begin{axis}[
yticklabel style={
/pgf/number format/.cd,
fixed,
fixed zerofill,
precision="<>ToString[decimall]<>",
},
scale only axis,
axis y line*=left,
xtick pos=left,
xscale="<>ToString[N@plotaspectratio]<>",
xmin="<>ToString[xmin]<>",xmax="<>ToString[xmax]<>",ymin="<>ToString[ymin]<>
",ymax="<>ToString[ymax]<>",
xlabel="<>xlabel<>",ylabel="<>ylabel<>",
ytick="<>ToString[lticks]<>"]\n";
textpos=StringJoin[Table["
\\node[] at (axis cs:"<>ToString[linepos[[z,1]]]<>","<>ToString[linepos[[z,2]]]<>
") {"<>linelabel[[z]]<>"};",{z,Length@temp}]];
line=StringJoin[Table["
\\addplot[color="<>If[ListQ[mycolor[[z]]],
ToString[mycolor[[z,1]]]<>","<>ToString[mycolor[[z,2]]],
ToString[mycolor[[z]]]]<>",mark=none,line width=0.5mm] coordinates{\n"
<>StringJoin["("<>ToString[#[[1]]]<>","<>ToString[#[[2]]]<>")\n"&/@temp[[z]]]<>
"};\n\\addlegendentry{$G_{0}= "<>ToString[G0[[z]]]<>"$}",{z,Length@temp}]]
<>"\n\\end{axis}\n";
axis2="\n\\begin{axis}[
yticklabel style={
/pgf/number format/.cd,
fixed,
fixed zerofill,
precision="<>ToString[decimalr]<>",
},
scale only axis,
axis y line*=right,
xtick pos=left,
xscale="<>ToString[N@plotaspectratio]<>",
xmin="<>ToString[xmin]<>",xmax="<>ToString[xmax]<>",ymin="<>ToString[ymin]<>
",ymax="<>ToString[ymax]<>",
ytick="<>ToString[rticks]<>"]\n";
"\\begin{tikzpicture}"<>axis1<>textpos<>line<>axis2<>"\n\\end{axis}\n\\end{tikzpicture}"
]
Mathematica 教學：使用 Jupyter Notebook 做為 Mathematica 操作環境
由 戴忠淵 於 2019年11月22日星期五
下午2:25 發表
安裝 Ijupyter
python3 -m pip install --upgrade pip python3 -m pip install jupyter
設定遠端連線 jupyter server，在python shell中執行
from notebook.auth import passwd; passwd()
生成修改設定檔
jupyter notebook --generate-config vi ~/.jupyter/jupyter_notebook_config.py c.NotebookApp.ip='*' #*表示所有IP，這裡設定ip為都可訪問 c.NotebookApp.password = '填寫剛剛生成的密文' c.NotebookApp.open_browser = False # 禁止notebook啟動時自動開啟瀏覽器 c.NotebookApp.port =9999 #指定訪問的埠，預設是8888。
下載 configure-jupyter.wls
https://github.com/WolframResearch/WolframLanguageForJupyter
執行 wolframscript 安裝 WolframLanguageForJupyter
wolframscript configure-jupyter.wls add啟動 Jupyter notebook
Excel 教學：符合條件整列變色
由 戴忠淵 於 2018年11月17日星期六
下午4:26 發表
Mathematica 教學：抓網頁特定資料
由 戴忠淵 於 2018年10月24日星期三
上午8:43 發表
xx=Import["http://www.fishbase.org/summary/Decapterus-maruadsi.html","Table"];
StringJoin[#<>""&/@Cases[xx,{"Fisheries:",___},Infinity][[1,1;;-2]]]
ThesisNoWorryMed Beta 0.2
由 戴忠淵 於 2018年6月11日星期一
上午8:45 發表
- MI值調整
- 項目分析報表修訂
- 三構面中介模型報表修訂
- 新增兩構面因果關係路徑模式
Temple trip
由 戴忠淵 於 2018年5月13日星期日
下午12:27 發表
Exporting graphics to TikZ format with Mathematica
由 戴忠淵 於 2018年2月9日星期五
下午6:04 發表
mytwoaxistikz[data__,{xmin_,xmax_,ymin_,ymax_},mycolor__,{xlabel_,ylabel_},{rticks__,lticks__},
linelabel__,linepos__,plotaspectratio_:1]:=Block[{temp=data,axis1,axis2,textpos,line},
axis1="
\\begin{axis}[
scale only axis,
axis y line*=left,
xtick pos=left,
xscale="<>ToString[N@plotaspectratio]<>",
xmin="<>ToString[xmin]<>",xmax="<>ToString[xmax]<>",
ymin="<>ToString[ymin]<>",ymax="<>ToString[ymax]<>",
xlabel="<>xlabel<>",ylabel="<>ylabel<>",
ytick="<>ToString[lticks]<>"]\n";
textpos=StringJoin[Table["
\\node[] at (axis cs:"<>ToString[linepos[[z,1]]]<>","<>
ToString[linepos[[z,2]]]<>") {"<>linelabel[[z]]<>"};",
{z,Length@temp}]];
line=StringJoin[Table["
\\addplot[color="<>If[ListQ[mycolor[[z]]],
ToString[mycolor[[z,1]]]<>","<>ToString[mycolor[[z,2]]],
ToString[mycolor[[z]]]]<>",mark=none,line width=0.5mm] coordinates{\n"
<>StringJoin["("<>ToString[#[[1]]]<>","<>ToString[#[[2]]]<>")\n"&/@temp[[z]]]<>"};",
{z,Length@temp}]]
<>"\n\\end{axis}\n";
axis2="\n\\begin{axis}[
scale only axis,
axis y line*=right,
xtick pos=left,
xscale="<>ToString[N@plotaspectratio]<>",
xmin="<>ToString[xmin]<>",xmax="<>ToString[xmax]<>",
ymin="<>ToString[ymin]<>",ymax="<>ToString[ymax]<>",
ytick="<>ToString[rticks]<>"]\n";
"\\begin{tikzpicture}"<>axis1<>textpos<>line<>axis2<>"\n\\end{axis}\n\\end{tikzpicture}"
]
ThesisNoWorryMed Beta 0.1
由 戴忠淵 於 2018年1月15日星期一
下午11:01 發表
ThesisNoWorryMed Beta 0.1
目前提供三個變數的中介模型，一次跑完以下分析：
- 三構面各分量表的項目分析
- 三構面各分量表的Cronbach's alpha 信度及一階CFA的聚合效度 (AVE) 、收斂信度 (CR)及區別效度。
- 三構面各分量表的人口統計差異性分析及事後比較。
- 三構面的階層回歸中介效果檢定分析。
- 三構面的結構方程式模型，SEM。
ThesisNoWorryMed[量表X, 量表M, 量表Y, X各分量表題數, Y各分量表題數, Z各分量表題數, X各分量表名稱, M各分量表名稱, Y各分量表名稱, 人口統計變數資料, 人口統計變數名稱]
ThesisNoWorryCFA[X, {5, 6, 4}, {X1, X2, X3}]
ThesisNoWorryMed[X, M, Y, {5, 6, 4}, {4, 5}, {3, 3}, {X1, X2, X3}, {M1, M2}, {Y1, Y2}, Dem, DemName]
Mathematica 教學：ListPlot with Histogram axes.
由 戴忠淵 於 2017年10月3日星期二
下午10:01 發表
data=RandomVariate[BinormalDistribution[{1,2},{1.5,2},0.6],10000];
ListPlot[data,PlotRange->{{-5,8},{-5,8}},Axes->None,
Frame->True,AspectRatio->1,ImageSize->350,
FrameLabel->{
{Automatic,
Histogram[data[[All,2]],{-5,8,0.5},AspectRatio->0.2,
Axes->None,BarOrigin->Top,ImageSize->275]},
{Automatic,
Histogram[data[[All,1]],{-5,8,0.5},AspectRatio->0.2,
Axes->None,BarOrigin->Bottom,ImageSize->275]}}
]
Show[DensityHistogram[data,{0.5},ColorFunction->(White&),
Method->{"DistributionAxes"->"Histogram"}],ListPlot[data]]
Mathematica 教學： Prove that 3/8< (1-cos(x)/cos(x/2))/x^2< 4/Pi^2 for all 0< x < Pi/2
由 戴忠淵 於 2017年9月19日星期二
下午8:52 發表
KKTMinimize[obj_,eqns_,ineqns_,variables_]:=
Block[{myrule,lambda,u,\[Lambda],Lagrange,eqnu,ineqnlam,
eqnus,ineqnlams,kkteqns,kktvars,kktans},
myrule={z_[i_]:>ToExpression[ToString[z]<>ToString[i]]};
eqnu=u[#]&/@Range[Length@eqns];
ineqnlam=\[Lambda][#]&/@Range[Length@ineqns];
eqnus=If[Length@eqns>=1,eqns.eqnu,0];
ineqnlams=If[Length@ineqns>=1,ineqns.ineqnlam,0];
kktvars=Flatten@{variables,eqnu,ineqnlam}/.myrule;
Lagrange=obj-eqnus-ineqnlams;
kkteqns=Flatten@{Thread[D[Lagrange,{variables}]==0],
Thread[eqns==0],Thread[ineqns<=0],
Thread[ineqns*ineqnlam==0],Thread[ineqnlam<=0]}/.
myrule;
If[MemberQ[PolynomialQ[#,kktvars]&/@kkteqns[[All,1]],False],
Print["KKT限制式均需為多項式。"],
kktans=Reduce[kkteqns,kktvars,
Backsubstitution->True]/.{And->List,Or->List,
Equal->Rule};
If[Length@Dimensions@kktans==1,{obj/.kktans,
kktans},{obj/.#,#}&/@kktans]]];
Plot[(1-Cos[x]/Cos[x/2])/x^2,{x,0.-10,Pi/2},
PlotRange->{{0,Pi/2},{0.3,0.5}},Frame->True,
FrameTicks->{{{0.3,0.5,{3/8,"3/8"},{4/Pi^2,"4/Pi^2"}},
None},{{0,Pi/2},None}},
GridLines->{None,{3/8,4/Pi^2}},GridLinesStyle->Dashed]
D[(1-Cos[x]/Cos[x/2])/x^2,x]//Simplify
D[(1-(Cos[x/2]^2-Sin[x/2]^2)/Cos[x/2])/x^2,x]//Simplify
D[4-4Sec[x/2]+3xTan[x/2]-4Tan[x/2]^2+xTan[x/2]^3,x]//TrigExpand//Simplify
(D[(6x-2Sin[x/2]-4Sin[x]-2Sin[(3x)/2]+Sin[2x]),x]//TrigExpand)
/.{Sin[z_]:>a,Cos[z_]:>b}
KKTMinimize[6+4a^2+2a^4-b+9a^2b-4b^2-12a^2b^2-3b^3+2b^4,{},
{-a,-b,a-1/Sqrt[2],1/Sqrt[2]-b,b-1},{a,b}]
Limit[(1-(Cos[x/2]^2-Sin[x/2]^2)/Cos[x/2])/x^2,x->0]
Limit[(1-(Cos[x/2]^2-Sin[x/2]^2)/Cos[x/2])/x^2,x->Pi/2]
Let f(x)=(1-cos(x)/cos(x/2))/x^2. Taking the first derivative of f(x) with respect to x yields d/dx f(x)=cos(x/2)*g(x)/(2x^3),
where g(x)=x*tan^3(x/2)-4*tan^2(x/2)+3*x*tan(x/2)-4*sec(x/2)+4. Because g'(x)=1/4*sec(x/2)^2*h(x) and h'(x)=k(x)=2*sin^4(x/2)+4*sin^2(x/2)+2*cos^4(x/2)-3*cos^3(x/2)-4*cos^2(x/2)-cos(x/2)-12*sin^2(x/2) *cos^2(x/2)+9*sin^2(x/2) cos(x/2)+6. Let a=sin(x/2) and b=cos(x/2). By Karush-Kuhn-Tucker conditions, we know that k(x) reaches its minimum at a=0 and b=1. This, together with the facts that h(0)=0, g(0)=0, and f(0)=0, indicates that f(x) is increasing in x, which also implies that 3/8<(1-Cos[x]/Cos[x/2])/x^2<4 br="" completes="" proof.="" the="" this="">
Mathematica 教學： Prove that 1 - 3 s^2 + (1 + s^2) Cosh[s] >0.
由 戴忠淵 於 2017年9月18日星期一
下午11:55 發表
Plot[1-3s^2+(1+s^2)Cosh[s],{s,0,Pi},Frame->True]
SeriesCoefficient[1-3s^2+(1+s^2)Cosh[s],{s,0,n}]
Normal[Series[1-3s^2+(1+s^2)Cosh[s],{s,0,5}]]
Minimize[2-(3s^2)/2+(13s^4)/24,s]
Solve[D[2-(3s^2)/2+(13s^4)/24,s]==0,s]
Since the coefficient in the n-th order of the taylor series of 1-3s^2+(1 + s^2)Cosh[s] is positive for every even term and is
zero for every odd term for all n>=3, it is obvious to see that 1-3s^2+(1+s^2)Cosh[s]>2-(3s^2)/2+(13s^4)/24>25/26, which implies that 1-3s^2+(1+s^2)Cosh[s]>0. This completes the proof.
Mathematica 教學：抓取證交所股價資料
由 戴忠淵 於 2017年7月23日星期日
下午11:36 發表
mydate[date_]:=Block[{temp},
temp=Import[
"http://www.twse.com.tw/exchangeReport/MI_INDEX.html?date="<>ToString@date<>"&type=ALLBUT0999",
"JSON"];
{("data1"/.temp)[[All,{1,2,4,5}]],("data5"/.temp)[[All,
{1,2,3,4,5,6,7,8,9,11}]]}]
mydate[20170719][[1]] // TableForm
mydate[20170719][[2]] // TableForm
test=Quiet@{
{ToExpression@StringJoin@Characters[ToString@#][[1;;4]],
ToExpression@StringJoin@Characters[ToString@#][[5;;6]],
ToExpression@StringJoin@Characters[ToString@#][[7;;8]]},
mydate[#][[1,4]]}&/@Map[ToExpression@
StringJoin[ToString/@{#[[1]],
If[#[[2]]<10>ToString[#[[2]]],ToString[#[[2]]]],
If[#[[3]]<10>ToString[#[[3]]],
ToString[#[[3]]]]}]&,
DayRange["2017/05/1","2017/07/21"][[All,1]]]//Parallelize;
DateListPlot[{#[[1]],
ToExpression@StringReplace[#[[2,2]],","->""]}&/@
Select[test,Length@#[[2]]==4&],Filling->Bottom]
Block[{tempdata},
tempdata={#[[1]],ToExpression@StringReplace[#[[2,2]],","->""]}&/@
Select[test,Length@#[[2]]==4&];
DateListPlot[tempdata,Filling->Bottom,
Epilog->{Red,PointSize[0.025],Point[{tempdata[[#[[1]]]][[1]],#[[2]]}]&/@
FindPeaks[tempdata[[All,2]]]}]]
ListPlot with Colormap
由 戴忠淵 於 2017年6月30日星期五
下午8:26 發表
mylistplot[data_, xrange_, yrange_, pointsize_, colormap_, imagesize_] :=
Module[{colors, styledData},
colors = ColorData[colormap] /@ Rescale[data[[All, 2]], yrange];
styledData = Style[#, colors[[#2]]] & @@@ Transpose[{data, Range[Length[data]]}];
ListPlot[
styledData,
PlotTheme -> "Detailed",
PlotStyle -> PointSize[pointsize],
PlotRange -> {xrange, yrange},
Frame -> True,
ImageSize -> imagesize*GoldenRatio,
PlotLegends -> Placed[
BarLegend[{colormap, yrange}, LegendMarkerSize -> imagesize,
LegendMargins -> {{0, 0}, {0, 0}}],Right
]
]
]
mylistplot[iris, {2, 4}, {0, 2.5}, 0.015, "TemperatureMap", 225]
Use R within Mathematica
由 戴忠淵 於 2017年6月22日星期四
下午10:22 發表
Needs["RLink`"]
(* For Mac and MMA 10*)
SetEnvironment[ "DYLD_LIBRARY_PATH" ->"/Library/Frameworks/R.framework/Resources/lib"]
InstallR["RHomeLocation" -> "/Library/Frameworks/R.framework/Resources", "RVersion" -> 3];
REvaluate["R.version.string"]
(* Load packages*)
REvaluate["library(psych);"]
REvaluate["library(nortest);"]
REvaluate["library(GenABEL);"]
(* 因素分析，主成分法萃取，變異及大化法轉軸 *)
myfac=Map[REvaluate["{xx<-principal(iris[,1:4],nfactors="<>ToString[#]<>",
rotate=\"varimax\");xx$loadings}"]&,{2,3,4}];
myfac
(* 輸出因素負荷矩陣 *)
Reverse[SortBy[myfac[[1,1]],{#[[1]],#[[2]]}&]]//TableForm
TableForm/@myfac[[All,1]]
(* 因素分析資料*)
fadata = {
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 4, 5, 6},
{1, 2, 1, 1, 1, 1, 2, 1, 2, 1, 3, 4, 3, 3, 3, 4, 6, 5},
{3, 3, 3, 3, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 5, 4, 6},
{3, 3, 4, 3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 5, 6, 4},
{1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 1, 1, 1, 1, 1, 6, 4, 5},
{1, 1, 1, 2, 1, 3, 3, 3, 4, 3, 1, 1, 1, 2, 1, 6, 5, 4}};
(* 定義資料*)
RSet["factor", Transpose@fadata];
(* 在R中計算相關係數矩陣，傳回MMA小數後四捨五入 *)
Round[REvaluate["cor(factor)"], 0.0001] // MatrixForm
(* 因素分析 *)
REvaluate["factanal(factor, factors = 3)$loadings"]
(* 輸出因素負荷矩陣 *)
TableForm[#[[1]], TableHeadings -> {None, #[[-1, -1, -1, -1]]}] & /@
{REvaluate["factanal(factor, factors = 3)$loadings"]} // Column
(* 迴歸分析 *)
REvaluate["{
data(iris)
reg <- lm( Sepal.Length ~ Species, data=iris )
summary.text <- capture.output(print( summary(reg)) )
}"]
StringJoin@Riffle[#, "\n"] &@REvaluate["{
data(iris)
reg <- lm( Sepal.Length ~ Species, data=iris )
summary.text <- capture.output(print( summary(reg)) )
}"]
(* 產生常態隨機變數 *)
mydata=REvaluate["rnorm(100,mean=0,sd=1)"]&/@Range[100];
(* MMA次數分配 *)
\[ScriptCapitalD] = HistogramDistribution[mydata[[1]]]
(* MMA PDF & CDF *)
GraphicsRow[DiscretePlot[#[\[ScriptCapitalD], x], {x, -4, 4, .01},
PlotLabel -> #] & /@ {PDF, CDF}]
(* shapiro test, ks.test *)
shapiro[data_] := Block[{temp},
RSet["temp", data];
REvaluate[
"{xx=shapiro.test(temp); yy=ks.test(temp,\"pnorm\",0,1); zz=lillie.test(temp);
c(xx$statistic,xx$p.value,yy$statistic,yy$p.value,zz$statistic,zz$p.value)}"][[1]] ]
RSet["rn1", RandomReal[{0, 10}, 1000]];
rn2 = RandomReal[NormalDistribution[0, 1], 1000];
REvaluate["rntransform(rn1)"] // Short
Histogram[#, Frame -> True] & /@ {rn2, REvaluate["rntransform(rn1)"]}
ShapiroWilkTest[#, {"TestStatistic", "PValue"}] & /@ {rn2, REvaluate["rntransform(rn1)"]}
(* 利用RCurl擷取網路資料 *)
gosspost[n_]:=REvaluate["
{library(RCurl);
curl<-getCurlHandle();
curlSetOpt(cookie=\"over18=1\",followlocation=TRUE,curl=curl);
url<-\"https://www.ptt.cc/bbs/Gossiping/index" <> ToString[n] <>
".html\";
html<-getURL(url,curl=curl)
}"][[1]];
Gossiping =
Cases[ImportString[
StringReplace[gosspost[#], {"\n" -> "", "\t" -> ""}],
"XMLObject"],
XMLElement[
"div", {"class" -> "r-ent"}, {XMLElement[
"div", {"class" -> "nrec"}, {XMLElement[
"span", {"class" -> "hl f2"}, {_}]}],
XMLElement["div", {"class" -> "mark"}, {}],
XMLElement[
"div", {"class" -> "title"}, {XMLElement[
"a", {"shape" -> "rect",
"href" -> postlink_}, {posttile_}]}],
XMLElement[
"div", {"class" -> "meta"}, {XMLElement[
"div", {"class" -> "date"}, {_}],
XMLElement[
"div", {"class" -> "author"}, {author_}]}]}] :> {postlink,
posttile, author},
Infinity] & /@ Range[20861, 20862, 1];
Flatten[Gossiping, 1] // TableForm
Thesis No Worry
由 戴忠淵 於 2017年4月6日星期四
下午2:11 發表
thesisnoworryhlm[構面1量表,構面2量表,構面3量表,{構面1各分量表題數},{構面2各分量表題數},{構面3各分量表題數},
{構面1各分量表變數名稱},{構面2各分量表變數名稱},{構面3各分量表變數名稱}]
thesisnoworryhlm[ddata[[All,1;;15]],ddata[[All,16;;24]],
ddata[[All,25;;30]],{5,6,4},{4,5},{3,3},
{X1,X2,X3},{M1,M2},{Y1,Y2}]
thesisnoworryanova[構面1量表,構面2量表,構面3量表,{構面1各分量表題數},{構面2各分量表題數},{構面3各分量表題數},
{構面1各分量表變數名稱},{構面2各分量表變數名稱},{構面3各分量表變數名稱},人口統計變量資料,{人口統計變量變數名稱}
thesisnoworryanova[ddata[[All,1;;15]],ddata[[All,16;;24]],
ddata[[All,25;;30]],{5,6,4},{4,5},{3,3},
{X1,X2,X3},{M1,M2},{Y1,Y2},
ddata[[All,{31,32,33}]],{"Sex","Age","Edu"}]
Thesis No Worry 程式資料檔
How to get the coefficient of polynomial function
由 戴忠淵 於 2016年10月3日星期一
下午6:52 發表
1+2Sin[2x]+3Sin[3x]+4Sin[4x]/.{Plus->List,Sin[y_]->1}
原生植物園
由 戴忠淵 於 2016年9月18日星期日
下午9:11 發表
