A Sustainable Dynamic Optimization Model of Pricing and Advertising in the Presence of Green Innovation Investment
Chung-Yuan Dye and Tsu-Pang Hsieh
Finally, the acceptance from EJOR has arrived. The Julia code for the numerical examples in this paper is provided below. Alternatively, you can also implement it directly in Julia. Please leave a message if you have any problems with the implementation of the code.
julia=StartExternalSession["Julia"]
ExternalEvaluate[julia,"
using JuMP,Ipopt
dp(x)=(140-3*x);
K1(y)=(y/5-y^2/1000);
f1(x)=100*exp(-0.03*x);
f2(x)=2*exp(-0.045*x);
v1=25;
v2=10;
omega=300;
c=16.5;
h=0;
z=0.8;
"];
dynCP11=ExternalEvaluate[julia, "
function dynCP11(G0,gamma1,gamma2,delta,k1coef,k2coef,e,r,varpi,n)
m1 = Model(Ipopt.Optimizer)
set_silent(m1)
#set_optimizer_attributes(m1, \"tol\" => 1e-4, \"max_iter\" => 100)
register(m1, :dp, 1, dp; autodiff = true)
register(m1, :K1, 1, K1; autodiff = true)
register(m1, :f1, 1, f1; autodiff = true)
register(m1, :f2, 1, f2; autodiff = true)
@variable(m1, p[1:n], start = 30)
@variable(m1, w[1:n], start = 10)
@variable(m1, u[1:n], start = 10)
@NLexpression(m1,newG[i=1:n],(1-delta)^(-1+i)*((1-delta)*G0
+sum((gamma1*u[j+1]^k1coef+gamma2*w[j+1]^k2coef)/((1-delta)^j)
for j = 0:i-1)))
@NLexpression(m1,newCE[i=1:n],f1(w[i])+f2(w[i])*dp(p[i])*K1(newG[i])-varpi)
@NLobjective(
m1,
Max,
sum(z^(i-1)*((p[i]-c-h/2)*dp(p[i])*K1(newG[i])
-v1*u[i]^2/2-v2*w[i]^2/2-e*newCE[i])
for i = 1:n))
for i = 1:n
@constraint(m1, p[i] >= c + h / 2)
end
for i = 1:n
@constraint(m1, p[i] <= 140 / 3)
end
for i = 1:n
@constraint(m1, w[i] >= 0)
end
for i = 1:n
@constraint(m1, u[i] >= 0)
end
for i = 1:n
@NLconstraint(m1, newCE[i] >= 0)
end
JuMP.optimize!(m1)
p_val = JuMP.value.(p)
w_val = JuMP.value.(w)
u_val = JuMP.value.(u)
G_val=(1-delta)*G0+gamma1*u_val[1]^k1coef+gamma2*w_val[1]^k2coef
CE=f1(w_val[1])+f2(w_val[1])*dp(p_val[1])*K1(G_val)
profit=(p_val[1]-c-h/2)*dp(p_val[1])*K1(G_val)
-v1*u_val[1]^2/2-v2*w_val[1]^2/2-e*(CE-varpi)
return[p_val,w_val,u_val,G_val,CE,profit,objective_value(m1)]
end"];
dynCP22=ExternalEvaluate[julia,"
function dynCP22(G0,gamma1,gamma2,delta,k1coef,k2coef,e,r,varpi,n)
m1 = Model(Ipopt.Optimizer)
set_silent(m1)
#set_optimizer_attributes(m1, \"tol\" => 1e-4, \"max_iter\" => 100)
register(m1, :dp, 1, dp; autodiff = true)
register(m1, :K1, 1, K1; autodiff = true)
register(m1, :f1, 1, f1; autodiff = true)
register(m1, :f2, 1, f2; autodiff = true)
@variable(m1, p[1:n], start = 30)
@variable(m1, w[1:n], start = 10)
@variable(m1, u[1:n], start = 10)
@NLexpression(m1,newG[i=1:n],(1-delta)^(-1+i)*((1-delta)*G0
+sum((gamma1*u[j+1]^k1coef+gamma2*w[j+1]^k2coef)/((1-delta)^j)
for j = 0:i-1)))
@NLexpression(m1,newCE[i=1:n],f1(w[i])+f2(w[i])*dp(p[i])*K1(newG[i])-varpi)
@NLobjective(
m1,
Max,
sum(z^(i-1)*((p[i]-c-h/2)*dp(p[i])*K1(newG[i])
-v1*u[i]^2/2-v2*w[i]^2/2-r*newCE[i])
for i = 1:n))
for i = 1:n
@constraint(m1, p[i] >= c + h / 2)
end
for i = 1:n
@constraint(m1, p[i] <= 140 / 3)
end
for i = 1:n
@constraint(m1, w[i] >= 0)
end
for i = 1:n
@constraint(m1, u[i] >= 0)
end
for i = 1:n
@NLconstraint(m1, newCE[i] <= 0)
end
JuMP.optimize!(m1)
p_val = JuMP.value.(p)
w_val = JuMP.value.(w)
u_val = JuMP.value.(u)
G_val=(1-delta)*G0+gamma1*u_val[1]^k1coef+gamma2*w_val[1]^k2coef
CE=f1(w_val[1])+f2(w_val[1])*dp(p_val[1])*K1(G_val)
profit=(p_val[1]-c-h/2)*dp(p_val[1])*K1(G_val)
-v1*u_val[1]^2/2-v2*w_val[1]^2/2-r*(CE-varpi)
return[p_val,w_val,u_val,G_val,CE,profit,objective_value(m1)]
end"];
mysol13[g0_,\[Gamma]1_,\[Gamma]2_,\[Delta]_,k1_,k2_,e_,r_,cap_]:=
Block[{n=40,numiter=100,iter=0,ans1,ans2},
Print[{Dynamic[iter],Dynamic[ans2]}];
NestList[(
iter=iter+1;
ans1=
SortBy[{
dynCP11[#[[4]],\[Gamma]1,\[Gamma]2,\[Delta],k1,k2,e,r,cap,n],
dynCP22[#[[4]],\[Gamma]1,\[Gamma]2,\[Delta],k1,k2,e,r,cap,n]},
Last][[-1]];
ans2={ans1[[1,1]],ans1[[2,1]],ans1[[3,1]],ans1[[4]],
ans1[[5]],#[[-1]]+0.8^(iter-1)*ans1[[6]]})&,
{0,0,0,g0,0,0},numiter][[2;;-1]]
]
myexample=mysol13[#[[1]],0.5,0.8,0.2,0.5,0.8,8,2,#[[2]]]&/@
Flatten[Table[{i,j},{j,{250,300,400}},{i,{10,40}}],1]
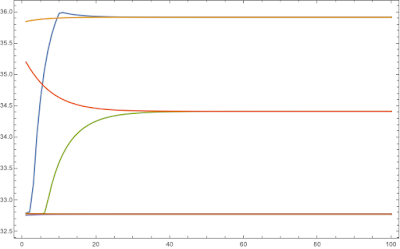
ListLinePlot[myexample[[All,All,#]],PlotRange->All,
Frame->True]&/@{1,2,3,4,5}//Column






讀者回應 ( 0 意見 )
訂閱發佈留言 (Atom)
發佈留言
Please leave your name and tell me what you thought about this site. Comments, suggestions and views are welcomed.
如果這篇文章對你有幫助,那請留個訊息給我~