Logistic regression
data={{1,0},{1,1},{1,1},{2,0},{2,0},{2,1},{2,1},{2,1},{2,1},{3,1},
{3,1},{3,1},{3,1},{3,1}};
(* 成功機率 *)
pi[x_]:=1/(1+Exp[-(a+b*x)])
(* Likelihood function*)
obj=Apply[Times,pi[#[[1]]]^#[[2]]*(1-pi[#[[1]]])^(1-#[[2]])&/@data]
(* 求解a and b *)
FindMaximum[Log[obj],{a,0.1},{b,0.1}]
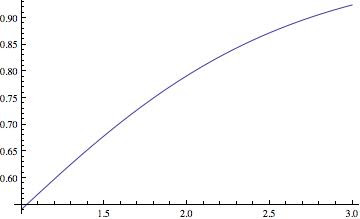
Plot[pi[x]/.FindMaximum[obj,{a,b}][[2]],{x,1,3},PlotRange->All]






讀者回應 ( 1 意見 )
訂閱發佈留言 (Atom)
I want to plot bifurcation diagram please help me
\[Sigma] = 0.1181;
\[Rho] = 4.5;
\[Eta] = 1; \[Mu] = 0.2; \[Delta] = 0.3743;
\[Alpha] = 1.636;
\[Beta] = 1;
ODE[tau_] := {x'[
t] == \[Sigma] + \[Rho]*x[t - tau]*
y[t - tau]/(\[Eta] + y[t - tau]) - \[Mu]*x[t]*y[t] - \[Delta]*
x[t], y'[t] == \[Alpha]*y[t]*(1 - \[Beta]*y[t]) - x[t]*y[t]};
st[tau_] :=
NDSolve[{ODE[tau], x[t /; t <= tau] == 0.1,
y[t /; t <= tau] == 0.1}, {x, y}, {t, 0, 500},
MaxSteps -> Infinity];
tmax = 200 ;
tmin = tmax - 50;
T = 2.0;
data0 = {};
data1 = {};
data2 = {};
data3 = {};
For[A1 = 0, A1 <= 3, A1 += 0.01,
dsol = st[A1];
xt = x[t] /. dsol[[1]];
For[t = tmin, t <= tmax, t += T,
AppendTo[data0, {A1, N[xt]}];
AppendTo[data1, {xt}]];
AppendTo[data2, {A1, Max[data1]}];
AppendTo[data3, {A1, Min[data1]}];
Clear[t]]; // AbsoluteTiming
f28 = ListPlot[{data2, data3}, PlotRange -> Automatic, Frame -> True,
Axes -> False, PlotStyle -> {Blue, Red}, Frame -> True,
PlotStyle -> {Blue, Red}, FrameLabel -> {"\[Tau]", "Immune Cells"}]
f29 = ListPlot[data0, PlotRange -> Automatic, Frame -> True,
Axes -> False, Frame -> True,
FrameLabel -> {"\[Tau]", "Immune Cells"}, PlotStyle -> {Green}]
發佈留言
Please leave your name and tell me what you thought about this site. Comments, suggestions and views are welcomed.
如果這篇文章對你有幫助,那請留個訊息給我~